Default Color Map: Difference between revisions
| (7 intermediate revisions by 2 users not shown) | |||
| Line 24: | Line 24: | ||
(Russ here) On the other hand, the rainbow map is in every case doing things that would be better done by a different map. The cognitive mapping, however easy, detracts from the primary task of understanding the data. The results of the bad mapping come into play in every real-world problem; they simply cannot be perceived and so are not known. The above argument means that our hope in using the rainbow map is that people are not using it for anything important so are not mislead into doing something major but only in minor ways. (Note that an intentionally-banded rainbow map with distinct colors for each band would retain the good qualities of the map and would have equally-spaced bands that could be used to estimate values much more precisely; some of the other maps listed below can do this, but none with as many bands. This would not make it isoluminant, but no isoluminant map can show high spatial frequency data.) | (Russ here) On the other hand, the rainbow map is in every case doing things that would be better done by a different map. The cognitive mapping, however easy, detracts from the primary task of understanding the data. The results of the bad mapping come into play in every real-world problem; they simply cannot be perceived and so are not known. The above argument means that our hope in using the rainbow map is that people are not using it for anything important so are not mislead into doing something major but only in minor ways. (Note that an intentionally-banded rainbow map with distinct colors for each band would retain the good qualities of the map and would have equally-spaced bands that could be used to estimate values much more precisely; some of the other maps listed below can do this, but none with as many bands. This would not make it isoluminant, but no isoluminant map can show high spatial frequency data.) | ||
There are undoubtedly some users who would rebel if the rainbow map were not available, but making it the default is encouraging poor choice. If I were making the decision, I'd rename the color map "misleading" to warn potential users of the dangers and provide a link to a good reference for color-map choice. | |||
[[Image:SpatialContrastHueWheel.png]] | [[Image:SpatialContrastHueWheel.png]] | ||
| Line 193: | Line 195: | ||
The results when using this color map are as follows. As you can see, it looks pretty good. In fact, it is hard to distinguish from the Brewer color maps (except for the Mach band in the center of the gray region, which makes it look like the torus has a thin band across it). | The results when using this color map are as follows. As you can see, it looks pretty good. In fact, it is hard to distinguish from the Brewer color maps (except for the Mach band in the center of the gray region, which makes it look like the torus has a thin band across it). | ||
<pre> | |||
<!-- This map goes from CIELab from <40,-5,-34> to <97,0,0> to <40,60,53> --> | |||
<ColorMap name="Linear CIELab 1" space="RGB"> | |||
<Point x="1" o="1" r="0.732691891" g="0.098811709" b="0.00679232" /> | |||
<Point x="0.875" o="1" r="0.831556904" g="0.365112385" b="0.247843798" /> | |||
<Point x="0.75" o="1" r="0.906621393" g="0.568733213" b="0.473912925" /> | |||
<Point x="0.625" o="1" r="0.953403586" g="0.766601281" b="0.713328364" /> | |||
<Point x="0.5" o="1" r="0.966006412" g="0.96603773" b="0.965934958" /> | |||
<Point x="0.375" o="1" r="0.76583663" g="0.813150205" b="0.869436965" /> | |||
<Point x="0.25" o="1" r="0.565570631" g="0.665714642" b="0.773984466" /> | |||
<Point x="0.125" o="1" r="0.355334722" g="0.524474908" b="0.679588113" /> | |||
<Point x="0" o="1" r="0.019390722" g="0.390501895" b="0.586262521" /> | |||
</ColorMap> | |||
</pre> | |||
[[Image:ColorMapSpatialContrastLinearCIELab1.png]] | [[Image:ColorMapSpatialContrastLinearCIELab1.png]] | ||
| Line 200: | Line 218: | ||
Just for completeness, I also tried a varient where I held the luminance constant. In theory, this is better because the luminance is no longer misleading and will not interfere with surface shading. However, as expected we end up with a washed out color map that looks very similar to | Just for completeness, I also tried a varient where I held the luminance constant. In theory, this is better because the luminance is no longer misleading and will not interfere with surface shading. However, as expected we end up with a washed out color map that looks very similar to | ||
what David Karelitz has already come up with (and we have already determined is a bad choice for a default color map). | what David Karelitz has already come up with (and we have already determined is a bad choice for a default color map). | ||
== Polar Coordinate Interpolation == | |||
After playing with several different interpolation schemes in an attempt to get rid of the Mach band, I decided that the most effective approach will be to use a polar coordinate type representation. That way I can sweep a vector through the space where the changes will be perceptually linear even though the individual components will not be. | |||
Unfortunately, CIELCH space is no good because the L* value is the same as the CIELAB space, and that is the value that is causing the Mach band during linear interpolation (or more specifically, when we change direction in piecewise interpolation). | |||
The first component of the polar coordinate space is M*, the magnitude of the value in CIELAB space. Ideally we would like to hold this constant and sweep it through space with consistent changes in the angle. This will give us the behavior we want. More specifically, we want to swing this vector from some color to the L* axis. Thus, it makes sense to have the second coordinate be the angle between the L*a*b* vector and the L* axis. This angle represents the saturation of the color, and thus I call it s*. A convenient choice for the third coordinate to be the same hue value as CIELCH, h*. Thus, the conversion from CIELAB space to M*s*h* space is | |||
<math> | |||
M* = \sqrt{L*^2 + a*^2 + b*^2} | |||
</math> | |||
<math> | |||
s* = \arccos\left(\frac{L*}{M*}\right) | |||
</math> | |||
<math> | |||
h* = \arctan\left(\frac{b*}{a*}\right) | |||
</math> | |||
Likewise, the reverse conversion from M*s*h* to CIELAB is | |||
<math> | |||
L* = M* \cos\left(s*\right) | |||
</math> | |||
<math> | |||
a* = M* \sin\left(s*\right) \cos\left(h*\right) | |||
</math> | |||
<math> | |||
b* = M* \sin\left(s*\right) \sin\left(h*\right) | |||
</math> | |||
One final issue I have with this approach is that when $M$ is large, which you want for the most noticeable changes, the interpolation has a tendency to leave the range of representable colors. For the case where one or more of the coordinates is above the maximal value, I found that uniformly scaling back the RGB values is an effective way to get back to the displayable range. If one or more of the values is less than 0, simply snapping those values to 0. This is not an optimal solution. It would be better to find the minimum distance in CIELAB space. But it is not clear to me what a quick and easy way to do this would be, and the current method seems to work well enough. Note that this is different then how the VTK conversion does it, so that will have to change. | |||
After some experimentation, I have pretty much settled on the following color map that goes from <95, 0.98, -1.25> to <95, 0, -> to <95, 0.98, 0.6>. | |||
<pre> | |||
<!-- This map uses the funny polar color space based off of CIE L*ab that I --> | |||
<!-- am tentatively calling Msh (magnitude, saturation, hue). The map goes --> | |||
<!-- from Msh <95, 0.98, -1.25> to <95, 0, ?> to <95, .98, 0.6>. --> | |||
<ColorMap name="Msh 3" space="RGB"> | |||
<Point x="0" o="1" r="0.07514311" g="0.468049805" b="1" /> | |||
<Point x="0.03125" o="1" r="0.247872569" g="0.498782363" b="1" /> | |||
<Point x="0.0625" o="1" r="0.339526309" g="0.528909511" b="1" /> | |||
<Point x="0.09375" o="1" r="0.409505078" g="0.558608486" b="1" /> | |||
<Point x="0.125" o="1" r="0.468487184" g="0.588057293" b="1" /> | |||
<Point x="0.15625" o="1" r="0.520796675" g="0.617435078" b="1" /> | |||
<Point x="0.1875" o="1" r="0.568724526" g="0.646924167" b="1" /> | |||
<Point x="0.21875" o="1" r="0.613686735" g="0.676713218" b="1" /> | |||
<Point x="0.25" o="1" r="0.656658579" g="0.707001303" b="1" /> | |||
<Point x="0.28125" o="1" r="0.698372844" g="0.738002964" b="1" /> | |||
<Point x="0.3125" o="1" r="0.739424025" g="0.769954435" b="1" /> | |||
<Point x="0.34375" o="1" r="0.780330104" g="0.803121429" b="1" /> | |||
<Point x="0.375" o="1" r="0.821573924" g="0.837809045" b="1" /> | |||
<Point x="0.40625" o="1" r="0.863634967" g="0.874374691" b="1" /> | |||
<Point x="0.4375" o="1" r="0.907017747" g="0.913245283" b="1" /> | |||
<Point x="0.46875" o="1" r="0.936129275" g="0.938743558" b="0.983038586" /> | |||
<Point x="0.5" o="1" r="0.943467973" g="0.943498599" b="0.943398095" /> | |||
<Point x="0.53125" o="1" r="0.990146732" g="0.928791426" b="0.917447482" /> | |||
<Point x="0.5625" o="1" r="1" g="0.88332677" b="0.861943246" /> | |||
<Point x="0.59375" o="1" r="1" g="0.833985467" b="0.803839606" /> | |||
<Point x="0.625" o="1" r="1" g="0.788626485" b="0.750707739" /> | |||
<Point x="0.65625" o="1" r="1" g="0.746206642" b="0.701389973" /> | |||
<Point x="0.6875" o="1" r="1" g="0.70590052" b="0.654994046" /> | |||
<Point x="0.71875" o="1" r="1" g="0.667019783" b="0.610806959" /> | |||
<Point x="0.75" o="1" r="1" g="0.6289553" b="0.568237474" /> | |||
<Point x="0.78125" o="1" r="1" g="0.591130233" b="0.526775617" /> | |||
<Point x="0.8125" o="1" r="1" g="0.552955184" b="0.485962266" /> | |||
<Point x="0.84375" o="1" r="1" g="0.513776083" b="0.445364274" /> | |||
<Point x="0.875" o="1" r="1" g="0.472800903" b="0.404551679" /> | |||
<Point x="0.90625" o="1" r="1" g="0.428977855" b="0.363073592" /> | |||
<Point x="0.9375" o="1" r="1" g="0.380759558" b="0.320428137" /> | |||
<Point x="0.96875" o="1" r="0.961891484" g="0.313155629" b="0.265499262" /> | |||
<Point x="1" o="1" r="0.916482116" g="0.236630659" b="0.209939162" /> | |||
</ColorMap> | |||
</pre> | |||
After converting this interpolation to RGB space, snapping into viewable values, and converting back, the plots of the values in CIE-L*ab space and and the magnitude of the derivative in CIELAB space look as follows. Note that the L*a*b* curve would look smother and the derivative magnitude would be flat were it not for this snapping to representable values. | |||
[[Image:ColorMapMshPlot3.png]] | |||
[[Image:ColorMapMshDerivMagPlot3.png]] | |||
And here again are our test images. | |||
[[Image:ColorMapSpatialContrastMsh3.png]] | |||
[[Image:ColorMapTorusMsh3.png]] | |||
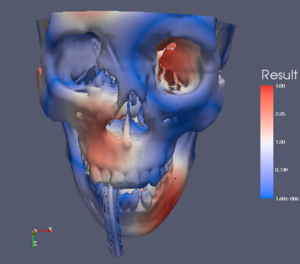
[[Image:ColorMapSkullMsh3.png]] | |||
== Table of Color Maps == | == Table of Color Maps == | ||
For reference and comparison, here is a table comparing all the color maps with three different data sets. From left to right, the data sets are: a spatial contrast sensitivity function, a torus with an elevation field, and a skull with a distracting scalar field. From top to bottom, the color maps are: rainbow, grayscale, black-body radiation, isoluminant red-green, isoluminant | For reference and comparison, here is a table comparing all the color maps with three different data sets. From left to right, the data sets are: a spatial contrast sensitivity function, a torus with an elevation field, and a skull with a distracting scalar field. From top to bottom, the color maps are: rainbow, grayscale, black-body radiation, isoluminant red-green, isoluminant CIELAB, three maps derived from the [http://www.colorbrewer.org ColorBrewer], a piecewise linear interpolation in CIELAB space, and a piecewise linear in M*s*h* space. | ||
{| | {| | ||
| Line 242: | Line 351: | ||
| [[Image:ColorMapTorusLinearCIELab1.png|300px]] | | [[Image:ColorMapTorusLinearCIELab1.png|300px]] | ||
| [[Image:ColorMapSkullLinearCIELab1.png|300px]] | | [[Image:ColorMapSkullLinearCIELab1.png|300px]] | ||
|- | |||
| [[Image:ColorMapSpatialContrastMsh3.png|300px]] | |||
| [[Image:ColorMapTorusMsh3.png|300px]] | |||
| [[Image:ColorMapSkullMsh3.png|300px]] | |||
|} | |} | ||
Latest revision as of 17:07, 13 June 2007
While at lunch recently I was flipping through a recent edition of IEEE Computer Graphics and Applications and came across the following article by David Borland and Russell M. Taylor II: "Rainbow Color Map (Still) Considered Harmful." The article iterates over all the well known ways that the rainbow color map fouls up visualization. What really caught my eye, though, was that ParaView was specifically mentioned.
Inspection or documentation indicated that ParaView, Matlab, VisAD, Ensight, Iris Explorer, and AVS Express all use the rainbow color map by default. Supplied tutorials indicated that SCIRun and OpenDX use the rainbow color map by default. Amira is the only program reviewed that does not use the rainbow color map by default.
It is a little bit embarrassing to be pointed out in a national article as a bad example for visualization. Still, we are also lumped into the same category as Ensight, AVS, and SCIRun (and VisIt was never even mentioned). Nonetheless, as a world leader in visualization it would be nice to do something better or, if we can't, have a pretty good reason why not. Thus, I started my quest to find that elusive "best" color map.
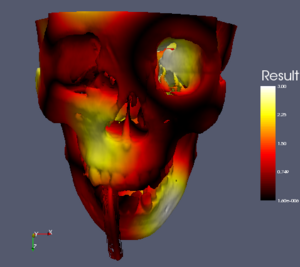
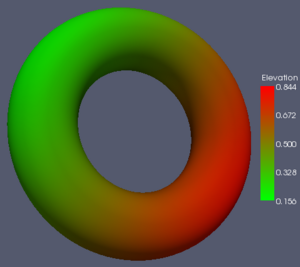
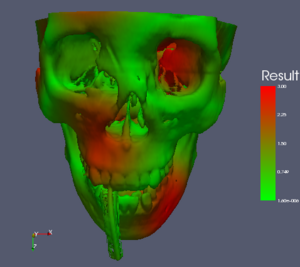
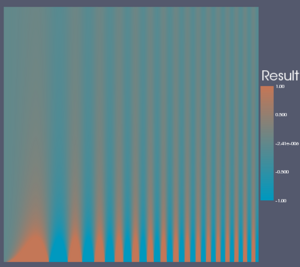
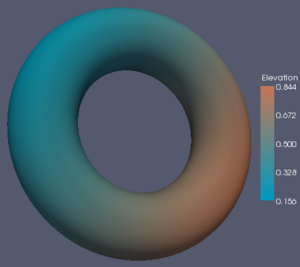
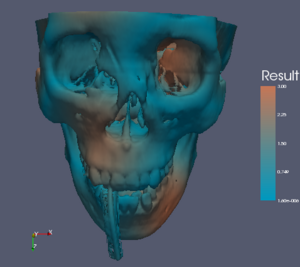
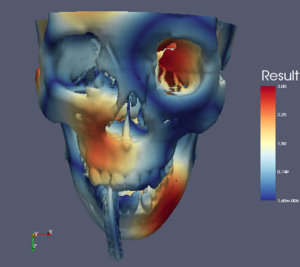
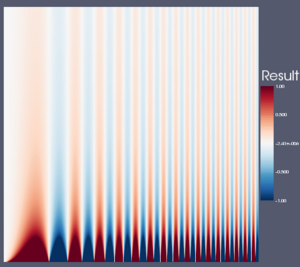
The rest of this Wiki page visits each color map in consideration and lists the pros and cons of each. It then gives an XML description of the color map that can be loaded into ParaView (unless it is already one of the default ParaView color maps) and shows image examples of the color map in use on three data sets. The first set is a spatial contrast sensitivity function. You will see frequency increasing to the right and contrast increasing to the bottom. This data set demonstrates the ability of the color map to show minimal contrast field changes. The second data set is a torus with the elevation filter applied to it. This data set can highlight banding caused by a color map. The third data set is a skull with a scalar field synthesized by summing the sine of the coordinates. I choose the scalar field in a way that would most interfere with the shading cues used to discern the shape of the object.
Rainbow Color Map
We all know and love (or hate) the rainbow color map. Adopted early on by physicists (who knew much more about electromagnetic radiation than human visual perception), it has become the rather unfortunate de-facto standard for visualization.
- Pros
-
- It is pretty. Although you will probably never see this mentioned as a factor in the literature, it can be pretty important in practice. Users will never choose ParaView if they feel our images are less "slick" than others.
- It has high ordinality. The rainbow passes through 5 distinct colors (blue, cyan, green, yellow, and red) and we could increase that to 6 if we chose to go down to violet. The colors visually separate the field into regions. Although the region boundaries are arbitrary and uneven, it nonetheless can simplify comparing regions.
- Cons
-
- The ordering is based on a physical phenomenon far removed from the visual perception of color. Experiments show that when human subjects are asked to order these colors, the results vary.
- Uneven perceptual changes. Equal increments in RGB or HSV space do not necessarily lead to equal perceptual increments. This leads to variation in widths of colors and occasional sharp transitions between colors, which leads to uneven bands in the color map. This can be actively misleading as there will be sharp transitions where there is none. It can also hide transitions that happen to fall within a band perceptually equivalent color. This is demonstrated in the spatial contrast sensitivity function below.
- Erratic luminance. The visual system perceives high spatial frequencies through changes in luminance, and luminance is often the best cue to ordering. However, the rainbow map is neither isoluminant nor ordered luminance. It goes from low luminance (blue) to high (cyan) to moderate (green) to high (yellow) to moderate (red).
That said, the rainbow color map is probably not as bad as indicated by the literature. The ordering is probably already ingrained in our users. We learn it pretty quickly. For example, my 6-year-old knows the colors of the rainbow in the proper order, consistently draws rainbows correctly, and has pointed out to me (without prompting) mistakes in other drawings. The perceptual problems introduced by the color map do not seem to bother many users either. I don't recall ever hearing a single complaint from users who go ballistic whenever data is inappropriately modified or misrepresented. In fact, one user told me that he was using rainbow pseudocoloring rather than grayscale on height field images knowing the perceptual problems involved with no explanation other than he simply "liked the colors". Perhaps the examples of bad mapping that we can easily construct do not often come to play in real-world problems.
(Russ here) On the other hand, the rainbow map is in every case doing things that would be better done by a different map. The cognitive mapping, however easy, detracts from the primary task of understanding the data. The results of the bad mapping come into play in every real-world problem; they simply cannot be perceived and so are not known. The above argument means that our hope in using the rainbow map is that people are not using it for anything important so are not mislead into doing something major but only in minor ways. (Note that an intentionally-banded rainbow map with distinct colors for each band would retain the good qualities of the map and would have equally-spaced bands that could be used to estimate values much more precisely; some of the other maps listed below can do this, but none with as many bands. This would not make it isoluminant, but no isoluminant map can show high spatial frequency data.)
There are undoubtedly some users who would rebel if the rainbow map were not available, but making it the default is encouraging poor choice. If I were making the decision, I'd rename the color map "misleading" to warn potential users of the dangers and provide a link to a good reference for color-map choice.
Grayscale and Black-Body Radiation Color Maps
The visual system is most sensitive to changes in luminance, so it comes as no surprise that a popular color map in literature is simply a grayscale that goes from black to white. This map is also popular in the medical field, although it may simply be an artifact of classical x-ray imagery being grayscale.
- Pros
- Clear perceptual ordering.
- High spatial contrast sensitivity.
- Cons
- Bad absolute resolution. The visual system interprets the luminance of a location relative to that its surroundings. Thus, it is difficult to get the absolute value represented by the color map. Experiments show that users produce errors of up to 20 percent (see Colin Ware's Information Visualization: Perception for Design).
- Inappropriate for 3D surfaces. Both this color map and 3D shading use changes in luminance. Thus, the two used together will interfere with each other. That makes this color map ineligible as a default for ParaView.
A similar color map is the black-body radiation color map, which mimics the visible color of a physical object as it is heated. At about 600 C, the object begins to glow a dull red. The color gets brighter as the object gets hotter, and the color moves from red to orange to yellow to white.
- Pros
- About all of the same pros as the grayscale.
- The colors add some information about the absolute value in the map.
- The images can look pretty slick.
- Cons
- The coloring ordering is opposite that of the rainbow color map that many people are used to, although the luminance should give enough indication of ordering.
- The black still interferes with shading, making it still inappropriate for 3D surfaces. In fact, the change in luminance across the board will confuse shading (as will any non-isoluminant map). Using the subset from dim red through white enables some shape perception on the entire object.
<ColorMap name="Black Body Radiation" space="RGB"> <Point x="0" o="1" r="0" g="0" b="0"/> <Point x="0.4" o="1" r="1" g="0" b="0"/> <Point x="0.75" o="1" r="1" g="1" b="0"/> <Point x="1" o="1" r="1" g="1" b="1"/> </ColorMap>
Isoluminant Color Maps
The fourth and last color map presented by the CG&A article was an isoluminant color map. The one given in the paper was a green-to-red isoluminant map which I have mimicked here. (Note: I was lazy and just did an RGB interpolation from <1,0,0> to <0,0,1>. It's not totally isoluminant --- specially at the ends --- but it is pretty close.) I also tried the "CIELab" isoluminant color map that has been with ParaView for many years now. I'm not sure on its origins, but it looks to be one of the better isoluminant color maps I have seen.
- Pros
- Does not interfere with shading.
- Relative comparisons are consistent.
- Visibly retrieving the values is relatively accurate.
- Cons
- They are butt ugly.
- They tend to look too dark.
- The visual system is not great as picking up small changes in hue. Thus, the effective resolution is low.
In short, I think these color maps would be quickly rejected by users.
(Russ here) They would be used by knowledgeable users who cared most about the data set mapped to the underlying geometry; a tutorial describing that luminance changes cannot be applied without modifying perceived shape would help produce more knowlegeable users. I agree that making it the default color map for 2D plots (or even for mapping onto surfaces) would be a mistake. No isoluminant color map can present high-frequency or low-contrast data changes.
Also note that the visual system doesn't use blue in its determination of luminance, so it is not possible to have saturated blue in a perceptually-isoluminant map. You can have a pastel blue if you mix the right amount of grey in to maintain luminance.
<ColorMap name="RedGreenIsoluminant" space="RGB"> <Point x="0" o="1" r="0" g="1" b="0"/> <Point x="1" o="1" r="1" g="0" b="0"/> </ColorMap>
Brewer Color Maps
The CG&A article left me a little flat. Having no better suggestion, it recommends an isoluminant color map for 3D surfaces. However, the isoluminant color maps have a fairly low perceptual resolution and, quite frankly, look like crap.
(Russ here) Having not enough space to give a complete description, it crammed that in as one of two choices at the end of the range from blackbody (best for 2d) and isoluminant (best if shape is what you care about). Colin Ware's book describes choices in great detail, as do Penny Rheingans' notes on her visualization page, and several other experts. The Colorbrewer map described below looks like an excellent middle ground, probably more useful for most mappings onto 3D surfaces than an isoluminant map (so long as mild distortion of the geomtetry can be lived with, which is certainly the case when the geometry is mostly providing context). For the default when mapping color onto a plane, blackbody will be better. For quantitative estimation, some sort of banded map (which provides isovalue contours) may be even better. (/Russ)
It did have another suggestion, though (one I have heard before), and that is to go to the ColorBrewer, which is basically a collection of color maps designed by color expert Cindy Brewer. The color maps are designed to be both aesthetically pleasing and contain changes that are perceptually consistent. Although the maps are designed to be used on a finite number of classes, I get around that by simply interpolating between colors (which may or may not be a good thing).
I picked divergent color maps (maps that go from color to neutral to color which separates values with a median point) mostly to maximize the range of colors. I went through three iterations. The first one looks good, but has a bit of a sickly yellow color in the middle. I then chose a similar map but with white in the middle. I think it looks nicer but may not be quite as smooth as the first. I was a little worried about how dark the ends were and how they effect shading, so I made a third version that goes to lighter colors. It reduces the luminance changes but also decreases the perceptual resolution. Like with all things it is a tradeoff.
- Pros
- Perceptual ordering is fairly intuitive. It goes from cool (blue) to neutral (white) to warm (red).
- It is similar to the rainbow color map. It is fairly similar to the current ParaView rainbow color map default except that we have swapped out the green for white. Users probably will not get upset by the change.
- It is aesthetically pleasing.
- It does not interfere too much with shading.
- It does not hide data in bands as much as the rainbow. Compare the images of the spatial contrast sensitivity function.
- Cons
- Lots of control points. Each one has 9 to 11 control points, which can be a hassle to users if they want to edit the color map. We may get around that some by doing interpolation in a perceptually linear space like CIELAB or CIELUV.
- It is not quite as sensitive to change as the grayscale map and interferes a little more with shading than the isoluminant maps. It also has less color separation than the rainbow. However, these are all conflicting requirements, and I think these color maps make a good compromise.
<ColorMap name="Candidate1" space="RGB"> <Point x="0" o="1" r="0.192157" g="0.211765" b="0.584314"/> <Point x="0.1" o="1" r="0.270588" g="0.458824" b="0.705882"/> <Point x="0.2" o="1" r="0.454902" g="0.678431" b="0.819608"/> <Point x="0.3" o="1" r="0.670588" g="0.85098" b="0.913725"/> <Point x="0.4" o="1" r="0.878431" g="0.952941" b="0.972549"/> <Point x="0.5" o="1" r="1" g="1" b="0.74902"/> <Point x="0.6" o="1" r="0.996078" g="0.878431" b="0.564706"/> <Point x="0.7" o="1" r="0.992157" g="0.682353" b="0.380392"/> <Point x="0.8" o="1" r="0.956863" g="0.427451" b="0.262745"/> <Point x="0.9" o="1" r="0.843137" g="0.188235" b="0.152941"/> <Point x="1" o="1" r="0.647059" g="0" b="0.14902"/> </ColorMap>
<ColorMap name="Candidate2" space="RGB"> <Point x="0" o="1" r="0.0196078" g="0.188235" b="0.380392"/> <Point x="0.1" o="1" r="0.129412" g="0.4" b="0.67451"/> <Point x="0.2" o="1" r="0.262745" g="0.576471" b="0.764706"/> <Point x="0.3" o="1" r="0.572549" g="0.772549" b="0.870588"/> <Point x="0.4" o="1" r="0.819608" g="0.898039" b="0.941176"/> <Point x="0.5" o="1" r="0.968627" g="0.968627" b="0.968627"/> <Point x="0.6" o="1" r="0.992157" g="0.858824" b="0.780392"/> <Point x="0.7" o="1" r="0.956863" g="0.647059" b="0.509804"/> <Point x="0.8" o="1" r="0.839216" g="0.376471" b="0.301961"/> <Point x="0.9" o="1" r="0.698039" g="0.0941176" b="0.168627"/> <Point x="1" o="1" r="0.403922" g="0" b="0.121569"/> </ColorMap>
<ColorMap name="Candidate3" space="RGB"> <Point x="0" o="1" r="0.129412" g="0.4" b="0.67451"/> <Point x="0.125" o="1" r="0.262745" g="0.576471" b="0.764706"/> <Point x="0.25" o="1" r="0.572549" g="0.772549" b="0.870588"/> <Point x="0.375" o="1" r="0.819608" g="0.898039" b="0.941176"/> <Point x="0.5" o="1" r="0.968627" g="0.968627" b="0.968627"/> <Point x="0.625" o="1" r="0.992157" g="0.858824" b="0.780392"/> <Point x="0.75" o="1" r="0.956863" g="0.647059" b="0.509804"/> <Point x="0.875" o="1" r="0.839216" g="0.376471" b="0.301961"/> <Point x="1" o="1" r="0.698039" g="0.0941176" b="0.168627"/> </ColorMap>
Perceptually Linearly Interpolated Color Maps
I am very encouraged by the resuls of using the Brewer color maps. In fact, as I think about it, I think some of the features that might normally be considered bad can actually be benifits. For example, the luminince goes from low to high in the middle to low again at the other end. As we look at an image, we can quickly spot out both the high and low extremes of luminance. Where are they? At the extrema of the data, which is often important. The third is in the middle, and the median value is as likely as any to be interesting.
My only reservation for this color map is the large number of control points. My hypothesis is that if we interpolate using a perceptually linear color space we can reduce the number of control points to 3. Obviously there will be one at each end. The third would be in the middle where the divergent color map has a singularity and the luminance and chromaticity change course. To start, I plotted the second Brewer color map in CIElab color space. (The EasyRGB web page has many convenient conversion functions and code.)
The luminance looks about what we would expect. It is maximal in the middle and moves down fairly straight to either side. The two chromatic plots are fairly straight in the middle, but vary a lot at the ends. I grabbed some values fairly arbitrarily in the middle and at both ends, then linearly interpolated in this space. In the blue end I picked <40,-5,-34>, in the middle I picked <97,0,0>, and in the red end I picked <40,60,53>. The resulting plot follows.
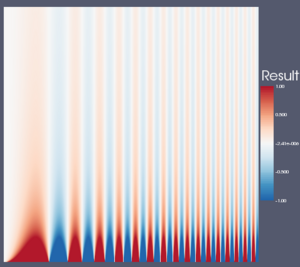
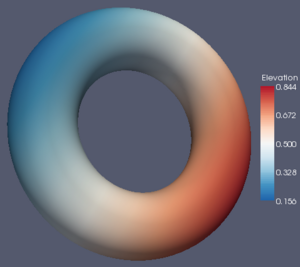
The results when using this color map are as follows. As you can see, it looks pretty good. In fact, it is hard to distinguish from the Brewer color maps (except for the Mach band in the center of the gray region, which makes it look like the torus has a thin band across it).
<!-- This map goes from CIELab from <40,-5,-34> to <97,0,0> to <40,60,53> --> <ColorMap name="Linear CIELab 1" space="RGB"> <Point x="1" o="1" r="0.732691891" g="0.098811709" b="0.00679232" /> <Point x="0.875" o="1" r="0.831556904" g="0.365112385" b="0.247843798" /> <Point x="0.75" o="1" r="0.906621393" g="0.568733213" b="0.473912925" /> <Point x="0.625" o="1" r="0.953403586" g="0.766601281" b="0.713328364" /> <Point x="0.5" o="1" r="0.966006412" g="0.96603773" b="0.965934958" /> <Point x="0.375" o="1" r="0.76583663" g="0.813150205" b="0.869436965" /> <Point x="0.25" o="1" r="0.565570631" g="0.665714642" b="0.773984466" /> <Point x="0.125" o="1" r="0.355334722" g="0.524474908" b="0.679588113" /> <Point x="0" o="1" r="0.019390722" g="0.390501895" b="0.586262521" /> </ColorMap>
Just for completeness, I also tried a varient where I held the luminance constant. In theory, this is better because the luminance is no longer misleading and will not interfere with surface shading. However, as expected we end up with a washed out color map that looks very similar to what David Karelitz has already come up with (and we have already determined is a bad choice for a default color map).
Polar Coordinate Interpolation
After playing with several different interpolation schemes in an attempt to get rid of the Mach band, I decided that the most effective approach will be to use a polar coordinate type representation. That way I can sweep a vector through the space where the changes will be perceptually linear even though the individual components will not be.
Unfortunately, CIELCH space is no good because the L* value is the same as the CIELAB space, and that is the value that is causing the Mach band during linear interpolation (or more specifically, when we change direction in piecewise interpolation).
The first component of the polar coordinate space is M*, the magnitude of the value in CIELAB space. Ideally we would like to hold this constant and sweep it through space with consistent changes in the angle. This will give us the behavior we want. More specifically, we want to swing this vector from some color to the L* axis. Thus, it makes sense to have the second coordinate be the angle between the L*a*b* vector and the L* axis. This angle represents the saturation of the color, and thus I call it s*. A convenient choice for the third coordinate to be the same hue value as CIELCH, h*. Thus, the conversion from CIELAB space to M*s*h* space is
<math> M* = \sqrt{L*^2 + a*^2 + b*^2} </math>
<math> s* = \arccos\left(\frac{L*}{M*}\right) </math>
<math> h* = \arctan\left(\frac{b*}{a*}\right) </math>
Likewise, the reverse conversion from M*s*h* to CIELAB is
<math> L* = M* \cos\left(s*\right) </math>
<math> a* = M* \sin\left(s*\right) \cos\left(h*\right) </math>
<math> b* = M* \sin\left(s*\right) \sin\left(h*\right) </math>
One final issue I have with this approach is that when $M$ is large, which you want for the most noticeable changes, the interpolation has a tendency to leave the range of representable colors. For the case where one or more of the coordinates is above the maximal value, I found that uniformly scaling back the RGB values is an effective way to get back to the displayable range. If one or more of the values is less than 0, simply snapping those values to 0. This is not an optimal solution. It would be better to find the minimum distance in CIELAB space. But it is not clear to me what a quick and easy way to do this would be, and the current method seems to work well enough. Note that this is different then how the VTK conversion does it, so that will have to change.
After some experimentation, I have pretty much settled on the following color map that goes from <95, 0.98, -1.25> to <95, 0, -> to <95, 0.98, 0.6>.
<!-- This map uses the funny polar color space based off of CIE L*ab that I --> <!-- am tentatively calling Msh (magnitude, saturation, hue). The map goes --> <!-- from Msh <95, 0.98, -1.25> to <95, 0, ?> to <95, .98, 0.6>. --> <ColorMap name="Msh 3" space="RGB"> <Point x="0" o="1" r="0.07514311" g="0.468049805" b="1" /> <Point x="0.03125" o="1" r="0.247872569" g="0.498782363" b="1" /> <Point x="0.0625" o="1" r="0.339526309" g="0.528909511" b="1" /> <Point x="0.09375" o="1" r="0.409505078" g="0.558608486" b="1" /> <Point x="0.125" o="1" r="0.468487184" g="0.588057293" b="1" /> <Point x="0.15625" o="1" r="0.520796675" g="0.617435078" b="1" /> <Point x="0.1875" o="1" r="0.568724526" g="0.646924167" b="1" /> <Point x="0.21875" o="1" r="0.613686735" g="0.676713218" b="1" /> <Point x="0.25" o="1" r="0.656658579" g="0.707001303" b="1" /> <Point x="0.28125" o="1" r="0.698372844" g="0.738002964" b="1" /> <Point x="0.3125" o="1" r="0.739424025" g="0.769954435" b="1" /> <Point x="0.34375" o="1" r="0.780330104" g="0.803121429" b="1" /> <Point x="0.375" o="1" r="0.821573924" g="0.837809045" b="1" /> <Point x="0.40625" o="1" r="0.863634967" g="0.874374691" b="1" /> <Point x="0.4375" o="1" r="0.907017747" g="0.913245283" b="1" /> <Point x="0.46875" o="1" r="0.936129275" g="0.938743558" b="0.983038586" /> <Point x="0.5" o="1" r="0.943467973" g="0.943498599" b="0.943398095" /> <Point x="0.53125" o="1" r="0.990146732" g="0.928791426" b="0.917447482" /> <Point x="0.5625" o="1" r="1" g="0.88332677" b="0.861943246" /> <Point x="0.59375" o="1" r="1" g="0.833985467" b="0.803839606" /> <Point x="0.625" o="1" r="1" g="0.788626485" b="0.750707739" /> <Point x="0.65625" o="1" r="1" g="0.746206642" b="0.701389973" /> <Point x="0.6875" o="1" r="1" g="0.70590052" b="0.654994046" /> <Point x="0.71875" o="1" r="1" g="0.667019783" b="0.610806959" /> <Point x="0.75" o="1" r="1" g="0.6289553" b="0.568237474" /> <Point x="0.78125" o="1" r="1" g="0.591130233" b="0.526775617" /> <Point x="0.8125" o="1" r="1" g="0.552955184" b="0.485962266" /> <Point x="0.84375" o="1" r="1" g="0.513776083" b="0.445364274" /> <Point x="0.875" o="1" r="1" g="0.472800903" b="0.404551679" /> <Point x="0.90625" o="1" r="1" g="0.428977855" b="0.363073592" /> <Point x="0.9375" o="1" r="1" g="0.380759558" b="0.320428137" /> <Point x="0.96875" o="1" r="0.961891484" g="0.313155629" b="0.265499262" /> <Point x="1" o="1" r="0.916482116" g="0.236630659" b="0.209939162" /> </ColorMap>
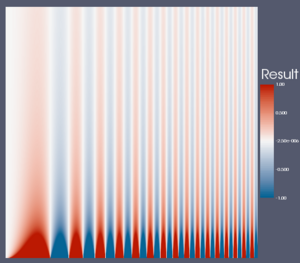
After converting this interpolation to RGB space, snapping into viewable values, and converting back, the plots of the values in CIE-L*ab space and and the magnitude of the derivative in CIELAB space look as follows. Note that the L*a*b* curve would look smother and the derivative magnitude would be flat were it not for this snapping to representable values.
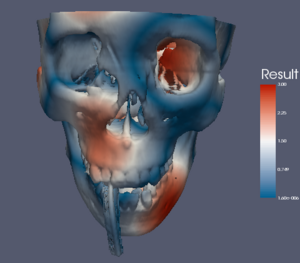
And here again are our test images.
Table of Color Maps
For reference and comparison, here is a table comparing all the color maps with three different data sets. From left to right, the data sets are: a spatial contrast sensitivity function, a torus with an elevation field, and a skull with a distracting scalar field. From top to bottom, the color maps are: rainbow, grayscale, black-body radiation, isoluminant red-green, isoluminant CIELAB, three maps derived from the ColorBrewer, a piecewise linear interpolation in CIELAB space, and a piecewise linear in M*s*h* space.

|

|

|

|

|

|

|

|
|

|
|
|
|
|
|

|

|
|
|

|

|
|
|

|
|

|
|

|

|
|