Plotting Over Curves

The Plot Edges filter sort and order polylines for graph visualization. The Plot Edges filter split, merge, any set of polylines to generate a more coherent set of point-ordered smoothed polylines. The points and cells of the output polylines are ordered in order to have a meaningful graph visualization of the point attributes.
In the example below, the polyline of the rectangle might be something like 1,3,5,7,...29,31,30,28...4,2,0.

Rectangle shaped polyline with points not ordered

Rectangle shaped polyline with points ordered

When branching and merging the polylines together, the focus

Use Case

Figure 1: Line Loop

Here's a possible use-case

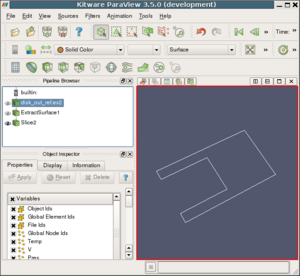
• Open disk_out_ref.ex2, load all variables
• Apply "Extract Surface" filter to disk_out_ref
• Apply "Slice" filter to "Extract Surface"

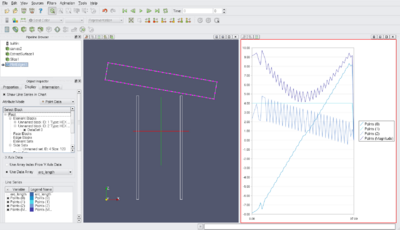
We get a nice line loop as shown in Figure 1. Now the user wants to create a plot of the data values along this curve.

Design

Write a new filter (let's call it vtkSortLines) that takes in a vtkPolyData as input and produces a vtkMultiBlockDataSet with vtkPolyData blocks as output. Each vtkPolyData in the output multiblock is a single connected poly-line with points (vtkPoints) ordered along the length of the poly-line i.e. you can traverse the poly-line by simply going through points 0 to (N-1) in the vtkPoints data structure without having to refer to the connectivity information for the poly-line.

The output from this filter can then directly plotting in a XY Plot View.

The vtkCutter with applied to poly-data input produces line segments. The first task for this filter is to merge connected line segments into a single poly-line. Once we have the poly-line then we can create the output vtkPolyData for each poly-line with ordered vtkPoints.

The algorithm can be summarized as:

Figure 2: Cases to be wary of

• Starting with a line segment, traverse connected line segments till you come to an end. Then start traversing in the reverse direction till you reach the other end to form the poly-line.
• If you encounter a loop, then, take the starting point as the point with min-X (or something consistent).
• Beware of branches and branches with loops as shown in Figure 2. In such cases we want to pick longest non-overlapping segments possible.